TREE

Tree
Merupakan salah satu bentuk struktur data tidak linear yang menggambarkan hubungan yang bersifat hirarkis (hubungan one to many) antara elemen-elemen. Tree bisa didefinisikan sebagai kumpulan simpul/node dengan satu elemen khusus yang disebut Root dan node lainnya terbagi menjadi himpunan-himpunan yang saling tak berhubungan satu sama lainnya (disebut subtree). Untuk jelasnya, di bawah akan diuraikan istilah-istilah umum dalam tree :
  1. Prodecessor : node yang berada diatas node tertentu.
  2. Successor : node yang berada di bawah node tertentu.
  3. Ancestor : seluruh node yang terletak sebelum node tertentu dan terletak pada jalur yang sama.
  4. Descendant : seluruh node yang terletak sesudah node tertentu dan terletak pada jalur yang sama.
  5. Parent : predecssor satu level di atas suatu node.
  6. Child : successor satu level di bawah suatu node.
  7. Sibling : node-node yang memiliki parent yang sama dengan suatu node.
  8. Subtree : bagian dari tree yang berupa suatu node beserta descendantnya dan memiliki semua karakteristik dari tree tersebut.
  9. Size : banyaknya node dalam suatu tree.
  10. Height : banyaknya tingkatan/level dalam suatu tree.
  11. Root : satu-satunya node khusus dalam tree yang tak punya predecssor.
  12. Leaf : node-node dalam tree yang tak memiliki seccessor.
  13. Degree : banyaknya child yang dimiliki suatu node
Binary Tree
Binary Tree adalah tree dengan syarat bahwa tiap node hanya boleh memiliki maksimal dua subtree dan kedua subtree tersebut harus terpisah. Sesuai dengan definisi tersebut, maka tiap node dalam binary tree hanya boleh memiliki paling banyak dua child.

Operasi-operasi pada Binary Tree :
  1. Create : Membentuk binary tree baru yang masih kosong.
  2. Clear : Mengosongkan binary tree yang sudah ada.
  3. Empty : Function untuk memeriksa apakah binary tree masih kosong.
  4. Insert : Memasukkan sebuah node ke dalam tree. Ada tiga pilihan insert: sebagai root, left child, atau right child. Khusus insert sebagai root, tree harus dalam keadaan kosong.
  5. Find : Mencari root, parent, left child, atau right child dari suatu node. (Tree tak boleh kosong)
  6. Update : Mengubah isi dari node yang ditunjuk oleh pointer current. (Tree tidak boleh kosong)
  7. Retrieve : Mengetahui isi dari node yang ditunjuk pointer current. (Tree tidak boleh kosong)
  8. DeleteSub : Menghapus sebuah subtree (node beserta seluruh descendantnya) yang ditunjuk current. Tree tak boleh kosong. Setelah itu pointer current akan berpindah ke parent dari node yang dihapus.
  9. Characteristic : Mengetahui karakteristik dari suatu tree, yakni : size, height, serta average lengthnya. Tree tidak boleh kosong. (Average Length = [jumlahNodeLvl1*1+jmlNodeLvl2*2+…+jmlNodeLvln*n]/Size)
  10. Traverse : Mengunjungi seluruh node-node pada tree, masing-masing sekali. Hasilnya adalah urutan informasi secara linier yang tersimpan dalam tree. Ada tiga cara traverse : Pre Order, In Order, dan Post Order.
Langkah-Langkahnya Traverse :
  • PreOrder : Cetak isi node yang dikunjungi, kunjungi Left Child, kunjungi Right Child.
  • InOrder : Kunjungi Left Child, Cetak isi node yang dikunjungi, kunjungi Right Child.
  • PostOrder : Kunjungi Left Child, Kunjungi Right Child, cetak isi node yang dikunjungi
BINARY SEARCH TREES (POHON CARI BINER)
Pohon cari biner adalah pohon biner yang dirancang untuk menskemakan urutan data yang akan dimasukkan ke dalam memori agar proses pencarian, penghapusan dan penambahan data dapat berjalan secara efisien dibanding dengan pemasukan data secara array maupun link.
Sifat dari skema pohon cari biner adalah : (1) setiap elemen yang berada di left substrees selalu lebih kecil dari elemen yang ada di right substrees, (2) setiap elemen yang berada di right substrees selalu lebih besar atau sama dengan elemen yang berada di left substrees.
Contoh : diketahui sekumpulan elemen sebagai berikut :
60, 75, 25, 50, 15, 66, 33, 44
Pembentukan awal skema pohon binernya berturut-turut sebagai berikut :
tree
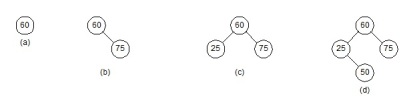
Gambar 11. Pembentukan Awal Pohon Cari Biner
dan, hasil akhirnya sebagai berikut :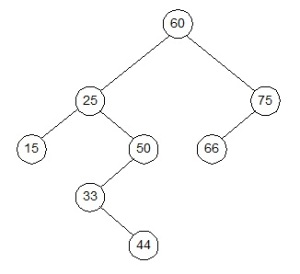
tree2
Gambar 12. Pohon Cari Biner



1.    Buat program untuk membanun tree berikut ini dan buatlah program tree traversal untuk membaca secara preorder, inorder dan postorder

Preorder: PFBAHMSRW
Inorder: ABFHMPRSW 
Postorder: ABMHFRWSP


2.    Buatlah program Tree Traversals untuk post order, in order dan pre order tapi tidak menggunakan rekursif.

ACC Tugas praktikum 7
Ø  Penjelasan class Binary Tree
·         __init__ ,berfungsi membuat sebuah binary tree dengan inputan satu data dan membuat 2 cabang kiri dan kanan dengan nilai cabang None.
·         insertLeft,memasukkan data barupadasuatucabangkiri.
·         insertRight,memasukkan data barupadasuatucabangkanan.
·         getLeftChild,melihat dan mengembalikan nilai dari cabang kiri.
·         getRighthild,melihat dan mengembalikan nilai dari cabang kanan.
·         setRootval,mengubah nilai data pada root  tertentu
·         getRootVal,melihat dan mengembalikan nilai dari root tertentu
A.      Penjelasan Program Tugas NO.1
1.       Membangun  tree
Analisis program :
·         Buat binary tree P dan tampung di variabel new
·         F pada cabang kiri pada Root new dan ditampung pada variabel F
·         S pada cabang kanan pada Root new dan ditampung pada variabel S
·         B pada cabang kiri pada Root F dan ditampung pada variabel B
·         A pada cabang kiri pada Root B dan ditampung pada variabelA
·         H pada cabang kanan pada Root F dan ditampung pada variabel H
·         M pada cabang kanan pada Root H dan ditampung pada variabel M
·         R pada cabang kiri pada Root S danditampungpadavariabel R
·         R pada cabang kanan pada Root S dan ditampung pada variabel W

Tree Tranversal Rekursif
a.       Post Order (left right value);
Analisis :
-          Rekursif dengan parameter anak cabang Kiri
-          Rekursif dengan parameter anak cabang Kanan
-          Print Root Value
b.      In Order (left value right);
Analisis :
-          Rekursif  dengan parameter anak cabang Kiri
-          Print Root Value
-          Rekursif dengan parameter anak cabang Kanan

c.       Pre Order(value left right);
Analisis :
-          Print Root Value
-          Recursive dengan parameter anakcabangKiri
-          Recursive dengan parameter anakcabangKanan

2.       Penejelasan Tugas Soal NO.2
Tree Tranversal Non Rekursif
a.       Post Order
Analisis :
1.       Inisialisai current dengan tree
2.       Lakukan push current kedalam stack
3.       Lakukan lopping sampai stackpertamakosong :
-          Inisialisasi current dengan pop dari stack pertama
-          Lakukan push value root dari current kedalam stack kedua
-          Jika cabang kiri ada nilainya maka lakukan push isi dari cabang kedalam stack
-          Jika cabang kanan ada nilainya maka lakukan push isi dari cabang kedalam stack
4.       Lakukan pengulangan sampai stack kedua kosong dan setiap looping lakukan print pop dari stack kedua
b.      In Order
Analisis :
1.       Inisialisai current dengan tree, dan done = False
2.       Looping sampai done == True :
-          Jika current berisi data makalakukan push current kedalam stack, kemudianinisialisai current dengananakcabangkiri current
-          Jika current tidakberisi data makaceklagi
-          Jika panjang stack lebihdari 0 maka :
a.       Inisialisasi current dengan pop dari stack
b.      Lakukan print current key atau root valuenya
c.       Inisilaisasicureentdengananakcabangkanan current
d.      Jikapanjang stack samadengan 0 atau empty makainisialisasi done == True maka looping Berhenti
c.       Pre Order
Analisis:
1.       Inisialisai current dengan tree
2.       Lakukan push current kedalam stack
3.       Lakukan lopping sampai stack kosong :
-          Inisialisai current =  pop dari stack
-          Print value root dari current tree
-          Jika cabang kanan ada nilainya maka lakukan push isi dari cabang kedalam stack
-          Jika cabang kiri ada nilainya maka lakukan push isi dari cabang kedalam stack
Agar ketika diprint anak cabang kiri keluar duluan
4.       Ketika Lopping  selesai maka semua data sudah terprint

from __future__ import print_function

class Stack:
    def __init__(self):
        self.items = []

    def isEmpty(self):
        return self.items==[]

    def push(self,items):
        self.items.append(items)

    def pop(self):
        return self.items.pop()

    def peek(self):
        return self.items[len(self.items)-1]

    def size(self):
        return len(self.items)
   
class Binarytree:
    def __init__(self,root):
        self.key = root
        self.leftChild = None
        self.rightChild = None

    def insertLeft(self,newNode):
        if self.leftChild == None :
            self.leftChild = Binarytree(newNode)

        else :
            t = Binarytree(newNode)
            t.leftChild = self.leftChild
            self.leftChild = t

    def insertRight(self,newNode):
        if self.rightChild == None :
            self.rightChild = Binarytree(newNode)

        else :
            t = Binarytree(newNode)
            t.rightChild = self.rightChild
            self.rightChild = t

    def getrightChild(self):
        return self.rightChild

    def getleftChild(self):
        return self.leftChild

    def getrootVal(self):
        return self.key

    def setrootVal(self,obj):
        self.key = obj

    def size(self):
        count = 0
        selfleft = self
        selfright = self
        while selfleft.getleftChild() != None or selfright.getrightChild() != None :
            count += 1
            if selfleft.getleftChild() != None:
                selfleft = selfleft.getleftChild()
            else :
                selfright = selfright.getrightChild()
        return count

   
def buildParseTree(fpexp):
    fplist = fpexp.split()
    pStack = Stack()
    eTree = Binarytree(" ")
    pStack.push(eTree)
    currentTree = eTree
    for i in fplist:
        if i == "(":
            currentTree.insertLeft("")
            pStack.push(currentTree)
            currentTree = currentTree.getleftChild()
        elif i not in ["P"]:
            currentTree.setrootVal(str(i))
            parent = pStack.pop()
            currentTree = parent
        elif i in ["P"]:
            currentTree.setrootVal(i)
            currentTree.insertRight("")
            pStack.push(currentTree)
            currentTree = currentTree.getrightChild()
        elif i == ")":
            currentTree = pStack.pop()
        else:
            return ("Error")
    return eTree

def Inorder(root):
    if root:
        Inorder(root.getleftChild())
        print(root.getrootVal(),end=" ")
        Inorder(root.getrightChild())

def Preorder(root):
    if root:
        print(root.getrootVal(),end=" ")
        Preorder(root.getleftChild())
        Preorder(root.getrightChild())

def Postorder(root):
    if root:
        Postorder(root.getleftChild())
        Postorder(root.getrightChild())
        print(root.getrootVal(),end=" ")

'''root = Binarytree('P')
root.insertLeft('F')
root.getleftChild().insertLeft('B')
root.getleftChild().insertRight('H')
root.getleftChild().getleftChild().insertLeft('A')
root.getleftChild().getrightChild().insertRight('M')
root.insertRight('S')
root.getrightChild().insertLeft("R")
root.getrightChild().insertRight("W")'''

print(r.getrootVal(),end = " ")
print(r.getleftChild().getrootVal(),end = " ")
print(r.getleftChild().getleftChild().getrootVal(),end = " ")
print(r.getleftChild().getleftChild().getleftChild().getrootVal(),end = " ")
print(r.getleftChild().getrightChild().getrootVal(),end = " ")
print(r.getleftChild().getrightChild().getrightChild().getrootVal(),end = " ")
print(r.getrightChild().getrootVal(),end = " ")
print(r.getrightChild().getleftChild().getrootVal(),end = " ")
print(r.getrightChild().getrightChild().getrootVal())
pt = buildParseTree( " ( P F B A H M S R W ) " )

Inorder(root)
print ()
Preorder(root)
print ()
Postorder(root)

Tidak ada komentar:

Posting Komentar

Langganan: Postingan (Atom)